Suppose you work at car dealership that owns makes and models of various manufacturers. Details of all those cars are maintained randomly in a book. Now when a customer walks in to buy a vehicle, you have to look up the cost of the car in that book. Here is how this conversation might go
- Customer: Do you have Nissan Maxima in your inventory?
- You: Let me take a look in my book.
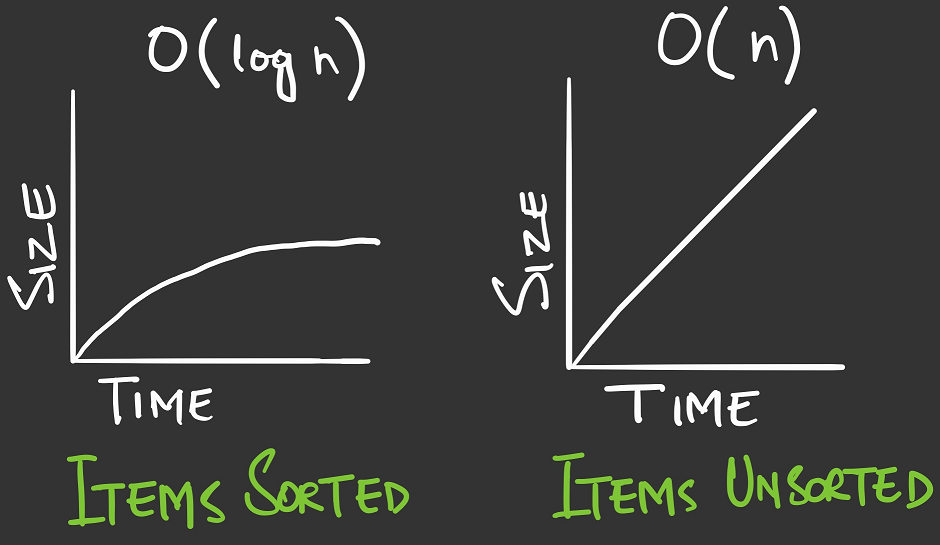
As you start going over the pages, line by line to search for the pricing, it’s quite obvious that your customer would be long gone. This is an example of linear search, which takes O(n) time. The larger the inventory the longer it takes because cars are maintained in no specific order.
| Car | Price |
|---|---|
| Toyota Camry | $20K |
| Audi RS | $50K |
| BMW 3 Series | $35K |
| Nissan Maxima | $30K |
Now if you would have maintained the inventory in an ordered listing you could have easliy performed a binary search, which takes O(log n) time because you can cut your search space and improve your time to look up a item in the inventory.
| Car | Price |
|---|---|
| Audi RS | $50K |
| BMW 3 Series | $35K |
| Nissan Maxima | $30K |
| Toyota Camry | $20K |
Binary and Linear Search Runtimes
In the upcoming post we will look at how we can go from O(log n) to O(1).